量子算法簡介
量子計算近年來受到了極大關注,根本原因在于其具有強大的并行性,可以在有效時間內解決一些經典計算機不能有效解決的問題。例如,Shor 算法可以在多項式時間內解決大數因子分解問題,從而對現代 密碼造成了極大威脅。然而,量子計算的并行性并非直接可以利用,而是需要根據所解決的問題經過巧妙的算法設計才可能。即便量子計算機研制成功,如果沒有相應的量子算法,量子計算的潛能還是得不到實質性發揮。因此,要想利用量子計算解決實際問題,能否設計出快速的量子算法是關鍵。不夸張的說,量子算法的研究是推動量子計算向前發展不可取代的力量源泉。
本文嘗試為大眾提供一個有關量子算法的通俗性介紹,主要內容如下:
量子計算并行性的根源
量子算法的基本框架
量子算法設計的困難性
量子算法研究簡明進程
關于量子算法的兩個疑問
總結
一、量子計算并行性的根源
量子計算并行性的根源何在?本文回答如下:
(1) 量子疊加帶來潛在的并行性。所謂量子疊加是指一個量子系統可以處于多個基態的線性組合形式,例如一個量子比特可以處于狀態a|0>+b|1>。由此,一次操作U可以并行作用于兩個態|0>和|1>上得到aU|0>+bU|1>,即所謂的“一次操作同時完成多次計算”。然而,這里在并行性前面加了定語“潛在的”,即這種并行性并非直接就解決了問題,還需要后續算法設計。正如量子計算知名學者Scott Aaronson在接受《麻省理工學院新聞》采訪時所說“你要是光看報、讀雜志等,你可能會覺得一個量子計算機可以通過‘并行地嘗試每一個可能的解’,然后‘在心臟跳一下的時間里解決NP完全問題’。嗯,大概那是門外漢們對于量子計算機最核心的錯誤印象。”
(2) 干涉(interference)使得并行性得以利用成為可能。中學物理課上大家都學習過一種物理現象叫做“雙縫干涉”,即一個單光源經過雙縫之后會在后面的屏幕上留下明暗相間的條紋。從數學上來看,干涉可以簡單理解為幾條不同的帶權重(權重可以取正、負數)的路徑匯合在一起的時候,權重可能相互抵消,也可能相互疊加增大。能否利用這種干涉現象使得量子計算并行性為我們所用,需要極具智慧的算法設計,關鍵就是要利用干涉現象使得我們想要的目標路徑的權重增大,而我們不希望出現的路徑權重抵消趨于零。

總結起來:量子疊加帶來潛在的并行性,干涉使得并行性得以利用成為可能,算法通過巧妙利用疊加與干涉發揮并行性解決實際問題。
二、量子算法的基本框架
設計量子算法的關鍵在于:要保證算法的每一步驟符合量子力學的要求,并最終保證其求解速度比經典算法更快。 能發揮量子計算并行性快速解決的問題在數學上通常是關于函數的某種全局屬性,所謂全局屬性即依賴于函數在某個區間中多個點處的函數值,例如函數的周期、再如下圖中的P(f)。
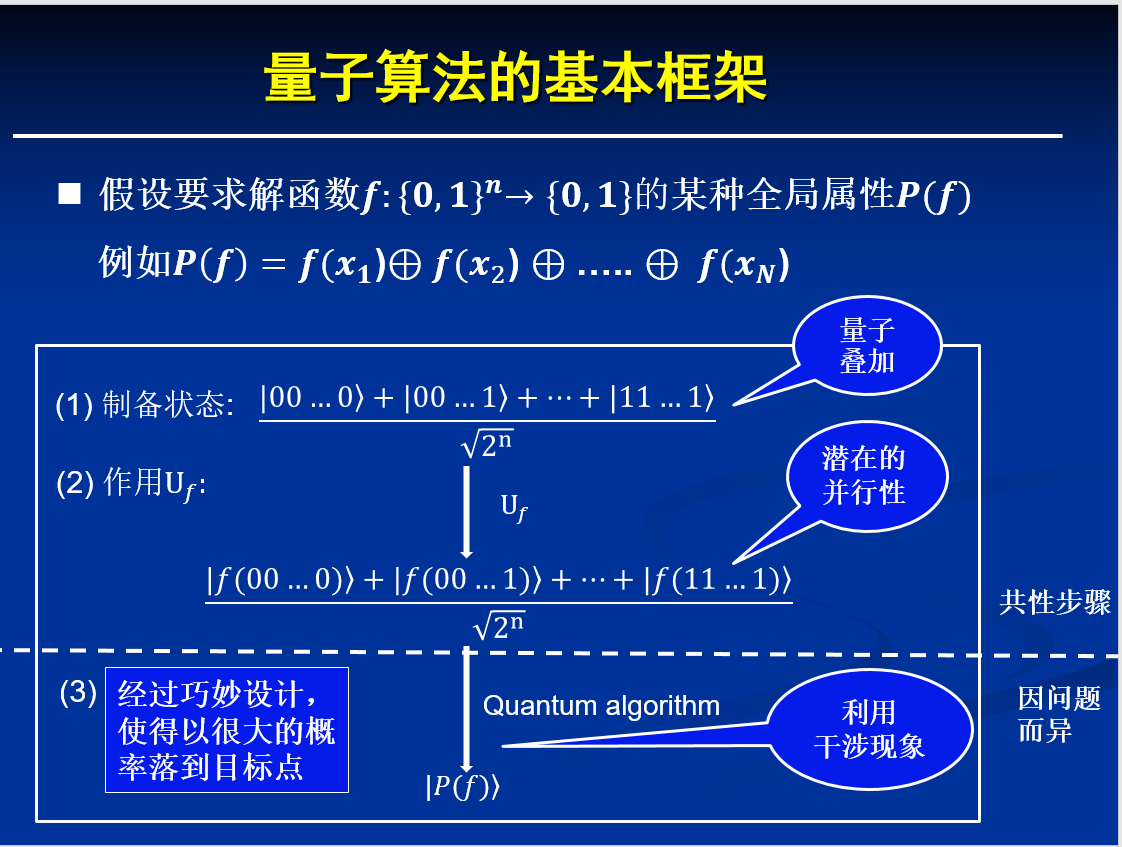
上圖中給出了量子算法的一般性框架,為了簡約性圖中可能去掉了一些嚴謹的細節。一個量子算法大致可以分為三個階段:
制備一個疊加態,它表示函數自變量值的線性組合;
作用U_f(函數f所對應的線性算子(矩陣)),根據線性性,它會分別作用在每一個基態上,把函數對每一個自變量的值計算出來,即體現潛在的并行性;
提取想要的信息。通過巧妙的設計,利用干涉現象使得系統最后狀態能以很大的概率落到目標點|P(f)>。算法設計的巧妙性就體現在這一步。
三、量子算法設計的困難性
要設計出好的量子算法并非易事,甚至可以說極具挑戰性。其困難性主要體現在以下兩點:
具有思想性的算法從來不容易,即使在經典計算領域也是如此。任何一個原創性算法都是智慧的結晶。
量子力學的反直觀性使得在經典世界積累的算法設計經驗可能不再適用,而此時還要求設計出比經典算法更好的量子算法,從而變得雪上加霜。目前人們并不太清楚量子計算能加速解決的問題具有什么特征,進行量子算法設計時基本上是摸著石頭過河。
四、量子算法研究簡明進程
雖然設計好的量子算法不易,但是研究者在這方面做了很多努力,也取得了一系列成果。經常有一種說法“現在就那么幾個量子算法”。這種說法在某種程度是對,因為具有代表性的量子算法確實不多。但換一個角度,以上說法又不太正確,因為目前針對不同應用場景的量子算法有上百個,大家可以參考http://quantumalgorithmzoo.org/ 了解目前一些主要的量子算法。
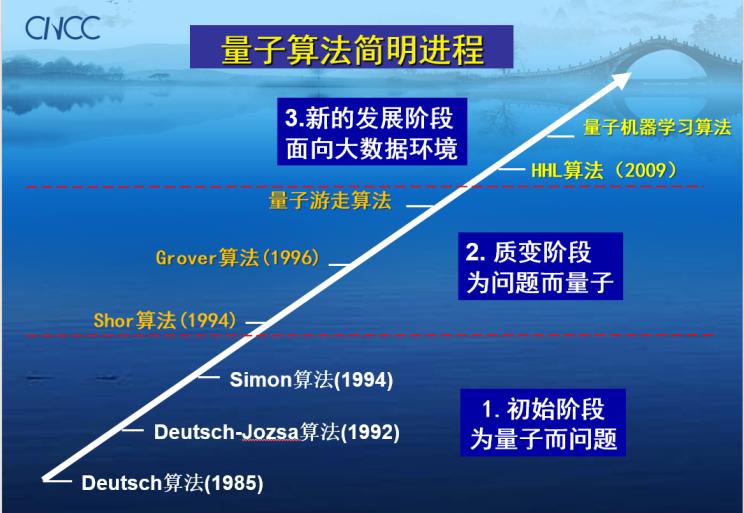
如上圖所示,追溯量子算法的歷史,大致可分為三個階段:
(1)量子算法的第一階段(1985-1994),我們稱之為初始階段,其特點是為量子而問題,即為了展示量子計算優勢而構造了一些數學問題并為之設計量子算法,這些問題在當時可能并沒有多少實用價值。最早的量子算法可以追溯到1985年的Deutsch算法。1985年David Deutsch在其關于量子圖靈機的開創性論文中給出了一個簡單問題,并為之設計了一個量子計算過程,通過利用量子疊加和干涉現象展現出了量子計算可能超越經典計算的優勢,這為后續量子算法設計埋下了思想的種子。雖然今天看來,Deutsch算法非常簡單,甚至會覺得一切都是理所當然的,但是在那前無古人的年代把第一個量子算法雛形設計出來是非常需要洞察力和創造力的。后來的Deutsch-Jozsa算法、Simon算法等進一步考慮更復雜的問題并在某種意義下展現出了量子計算相對于經典計算的指數加速優勢。
關于Simon算法多說幾句。這可能是一個有點被外界忽略的量子算法。事實上該算法的意義至少有以下兩方面:
Simon算法直接啟發了著名的Shor算法的發現,這一點無論是在Shor算法的原文還是在一些知名學者寫的量子計算方面的書里都有非常明確地指出來。
Simon算法近年在密碼破譯方面得到直接應用。雖然它所解決的問題在提出之初并未見明顯的應用場景,然而近幾年基于Simon算法進行密碼破譯的研究在不斷跟進,在密碼學頂級會議Crypto上就有相關工作發表。
有趣的是,Simon算法的作者Daniel R. Simon似乎除了提出該算法之外并沒有其他關于量子計算的成果。或許他只是在量子計算的花園里丟下一顆種子就走的游客,幸運的是種子已經發芽開花。
(2)量子算法的第二階段(1994-2009),我們稱之為質變階段,其特點是為問題而量子,即針對具有重要應用價值的問題而設計量子算法。1994年,Shor算法展示了大數分解問題可以被量子計算機在多項式時間內解決,而該問題在經典計算機下的難解性是RSA公鑰密碼系統安全性的理論基礎。隨后,1996年Grover發現了無序數據庫搜索的平方加速量子算法,使得在無序數據庫中“大海撈針”成為可能。由于這些算法所解決的問題具有廣泛的應用價值,使得這些算法備受關注,從而也大大推動了整個量子計算領域的發展。后續不少研究就是聚焦于如何把以上兩個算法映射到更多具有實際價值的問題。另外,此階段提出的量子游走也是一類進行量子算法設計的重要工具。
(3)量子算法的第三個階段(2009-至今),我們稱之為新的發展階段,其特點是面向大數據環境。2009年解線性方程組量子算法(HHL算法)的提出標志著量子算法進入了第三階段。或許HHL算法并不能與Shor算法或Grover算法媲美,但是在大家苦苦等待新的量子算法出現達10多年之久,HHL算法不失為量子算法設計提供了一條新路徑,它或許是把量子模擬應用于數據處理的范例。量子模擬是量子計算的一個重要方面,也涉及各種模擬算法的研究,不過由于其與物理過程更相關,而本文更側重于利用量子技術進行經典數據處理,所以此處不作重點介紹。
由于人工智能與大數據領域的諸多方法和技術都與解線性方程組有關,因此HHL算法的提出大力推動了量子計算進入機器學習與大數據處理等領域。量子計算與AI的結合近幾年成為熱點話題,圖靈獎得主姚期智先生也多次在報告中提及,毫無疑問這方面的交叉研究值得進行深入探索。
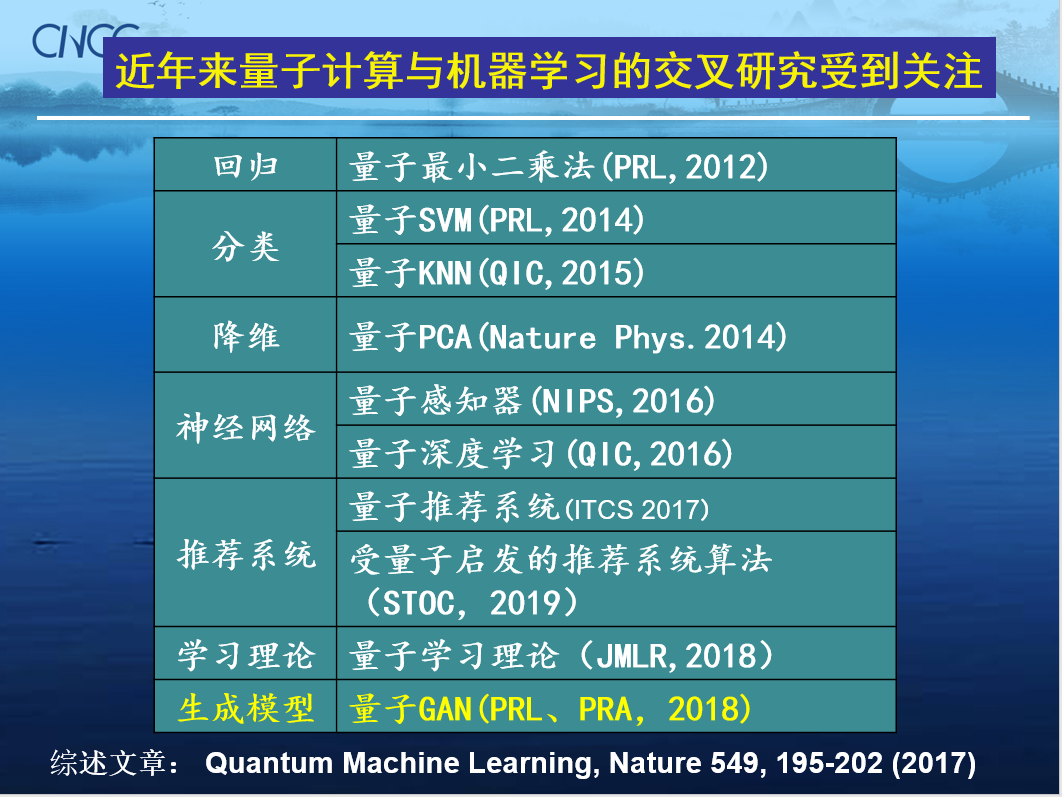
不過這里需要指出幾點:
HHL算法并未把方程組的解以經典可讀取的方式呈現出來,而是把其編碼在量子態中,需要經過后續的算法設計來提取我們想要的信息。近年來出現的大量有關量子機器學習的研究主要就是基于HHL算法做后續算法設計。
目前一些量子機器學習方面的研究需要提供更嚴肅的理論分析。
量子機器學習如果要面對實際數據處理問題,有待突破輸入/輸出瓶頸。所謂輸入/輸出瓶頸是指,目前大部分量子機器學習算法或者需要把大規模數據集編碼為量子態,或者只是把問題的解生成在量子態中,因此輸入階段的前處理和信息提取階段的后處理將耗費大量時間,乃至抵消量子算法所節省的時間。
近期,華裔學生 Ewin Tang 受量子推薦算法的啟發設計出了一個經典算法,它能以和量子算法相近的速度解決推薦問題,從而使得受量子啟發的經典算法設計或者說量子算法的經典化進入了更多學者的視野。在某些問題上量子被證明相對于經典有加速優勢,而更多的問題并沒有蓋棺定論,如果量子算法思維能促進經典算法的發展,這也將是量子計算研究意義的另一種體現。
五、關于量子算法的兩個疑問
筆者在平時交流中經常被問及以下兩個問題,特別是信息學背景的朋友問得比較多,相關問題和回答如下:
(1)量子計算機沒造出來,有必要研究量子算法嗎?
從經典計算領域來看,算法的研究遠遠早于計算機的出現。歐幾里德算法出現在古希臘時代,而第一臺電子計算機是1946年生產的。另外,圖靈機的提出正是為了嚴格地刻畫“算法”。
沒有算法支持的量子計算機是否還能稱為計算機呢?量子算法是量子計算機的必要軟件支撐,同時量子算法的研究也是推動量子計算發展的強大動力,從Shor算法的歷史地位可見一斑。
(2)沒有量子計算機,怎么研究量子算法?怎么評價算法的好壞?
抽象層次的算法設計從來不依賴于具體硬件平臺,在經典計算領域就是如此。算法本質上是解決問題的一種方法,量子算法是遵循量子力學規律的一種方法。硬件平臺只是實現這種方法的一個工具。當然,軟硬件之間的互動與交流對于設計更符合實際情況的算法非常必要。
從算法與復雜性研究的角度來看,算法的好壞由復雜度衡量,這依賴于嚴格的數學證明,而不是在具體硬件平臺上的測試。目前量子算法主流的研究是如此。
六、總結
量子計算機相對與經典計算機在哪些方面有優勢?有多大程度的優勢?這些問題目前遠未搞清楚,這意味著量子算法的研究有非常大的空間。大家都期待量子計算領域有更多具有創新性的算法出現,每一位量子算法研究者也都希望設計出一個代表性算法。然而,羅馬不是一天建成的,千里之行始于足下。我們不應只記住Shor算法的巧妙,而忘記前人的努力。事實上,Shor算法是站在Simon算法的肩上,而Simon算法源于那些看似沒用的Deutsch-Jozsa算法和Deutsch算法。這個過程正好體現了科學研究的魅力:或許很多研究成果會被大浪淘沙,但正是那些一點一滴的看似無用的研究一步一步孕育著一個新的發現!
最后一句:量子計算研究要“軟硬兼施“!
研究團隊介紹:
本文來自中山大學數據科學與計算機學院量子計算實驗室(http://www.sdshimeng.com/team/quantumlab),研究團隊主要研究興趣為量子計算模型、算法與復雜性,主要從計算機科學角度出發,圍繞”量子計算相對于經典計算有何優勢與本質不同”這一中心問題開展研究。
中山大學計算機學科從2000年左右開始從事量子計算方面的研究,是國內計算機領域最早從事量子計算研究的力量之一,已培養量子計算方面的研究生數十人,未來將一如既往地為量子計算的研究和人才培養做出努力。如果您是對量子計算感興趣的學生,歡迎一起來探索量子計算領域有趣的問題。如果您已學業有成,歡迎加入中山大學,我們一直在致力于團隊建設。期待有志青年加入,攜手共創未來!
研究團隊招聘專任教師、特聘研究員、副研究員、博士后,歡迎從事量子計算相關研究的青年才俊加入!招收博士、碩士、高年級本科。歡迎聯系咨詢(李綠周:lilvzh@mail.sysu.edu.cn),同時可以搜索微信公眾號“中山大學數據科學與計算機學院”了解相關招聘信息。


