由中山大學李綠周、北京郵電大學高飛、南京大學姚鵬暉、中科院計算所田國敬等幾位老師及相關團隊成員(北郵潘世杰,中大何鍵浩、葉澤坤)共同撰寫的《CCF2019-2020中國計算機科學技術發展報告》之題為“量子算法與復雜性研究進展概述”的章節近日正式出版。雖然紕漏難免,但愿如文中所言“希望本文能夠讓更多計算機、 物理、數學等相關領域的研究人員更好地了解量子計算理論方面的進展,借此也呼吁更多的學者和青年學生加入這個極具挑戰性的研究領域"
以下摘錄引言部分,全文初稿見附件。如果成為CCF會員,可在中國計算機學會(CCF)官網訪問機械工業出版社正式出版的電子版全文以及更多豐富的學術資源。
引用文章內容請標注:
李綠周,高飛,姚鵬暉,田國敬,何鍵浩,潘世杰,葉澤坤,量子算法與復雜性研究進展概述,CCF2019-2020中國計算機科學技術發展報告/ 中國計算機學會編,p. 1-59,機械工業出版社,2020.10.
毋庸置疑,量子計算作為一種顛覆性技術已經引起了各界的廣泛關注。然而需指出是,就可計算性而言量子計算并沒有超越經典計算,但就計算復雜性來說量子計算展現出巨大的優勢。例如,Shor量子算法可以在多項式時間內解決大數因子分解問題,從而在理論上對現代密碼造成了極大威脅。量子計算相對于經典計算在哪些方面有優勢?有多大程度的優勢?這些問題都遠未搞清楚,需要持續深入地研究。相比于廣闊的未知領域,目前能展現量子計算優勢的例證不是太多,而是太少。探尋量子優勢是量子計算研究的核心問題之一,有待廣大研究者去發現新的大陸。
從理論計算機科學的角度來看,至少可以從以下一些不同的視角來探尋量子計算的優勢:
查詢復雜性。關注計算過程調用某一子過程的次數,而忽略其他計算代價。目前量子計算相對于經典計算的優勢很多時候是通過查詢復雜度得以體現,例如著名的Grover算法。這方面有一套比較系統的分析查詢復雜度上下界的方法,并且量子計算的優勢可以從查詢復雜性角度得以嚴格證明。
交互計算復雜性。 關注多個計算個體協同完成某一個任務,由于信息不完備或者計算個體不可靠而產生的復雜性現象,包括交互式證明系統和通信復雜性。量子計算在這個模型中有著獨特的優勢。這方面目前已經取得了一系列重要成果。
時間復雜性。關注計算過程所耗費的時間,如Shor算法就在時間復雜度上展示出相對于目前最好的經典算法的優勢。不過,從時間復雜性的角度目前暫時無法嚴格證明量子計算對于經典計算的優勢,這與計算復雜性領域的重大理論問題P是否等于NP緊密相關。盡管如此,這并不妨礙開展量子計算研究,因為發現比目前最好的經典算法更好的量子算法總是一件振奮人心的事情。
樣本復雜性。關注在學習某一個目標函數的過程中需要用到多少樣本數據,這是學習理論領域研究的重要問題。近幾年研究人員初步考慮了量子學習理論方面的問題,主要是通過比較量子樣本復雜性與經典樣本復雜性來刻畫量子計算的優勢。總的來說,量子計算在這方面的研究有待加強。
電路深度復雜性。關注邏輯電路中邏輯門的層數,即如何盡可能并行化地完成計算。量子計算相對于經典計算的優勢可以在電路深度復雜性方面得以展示,例如最近Science上就有工作表明:存在計算問題能被常數深度的量子電路解決,而任意常數深度的經典電路不可能以高成功概率解決。
除此之外,還可以考慮有限自動機(狀態變遷系統)的狀態復雜性,這方面早就有研究成果表明:量子有限自動機相對于經典自動機在狀態復雜性方面可以有指數性優勢,有興趣的讀者可參考文獻[1][2][3],本文不對此進行詳細介紹。
本報告主要集中關注與以上五個方面相關的量子計算理論的研究進展。同時必須要指出的是,無論從哪個角度來展示量子計算優勢,都離不開量子算法,因為要說明量子計算有優勢,通常需要設計一個量子算法過程去求解問題。由此可見,量子算法是量子計算的靈魂。從量子計算的發展史來看, 正是Shor算法的提出引起了學術界對量子計算的廣泛關注。我們也堅信,未來必將由于量子算法的新突破帶來量子計算領域的進一步發展。當然,量子算法需要運行在量子計算硬件平臺上才能發揮優勢。因此,量子計算研究要“軟硬兼施”[4]。
圍繞“算法”和“復雜性”兩個關鍵詞,本報告將從量子查詢算法及復雜性、量子交互計算復雜性、量子機器學習、量子優化算法、量子電路優化與經典模擬等五個量子計算理論的主要研究方向進行闡述,分析與比較近年國內外研究進展,并對未來發展趨勢進行展望。與本報告內容相關的中文綜述性文獻可參考[5]。下面對本文涉及到的主要內容進行概要性介紹。
量子查詢算法及復雜性。這方面的主要研究可以概括為兩方面:(1)通過設計精巧的量子查詢算法展示量子計算優勢,目前這方面取得了豐碩研究成果。事實上關于量子算法的研究很多時候都是從查詢復雜度性角度進行討論。(2)分析量子查詢復雜性下界,目前已經得到一系列求解量子查詢復雜性下界的方法,包括多項式方法、對手法、半正定規劃方法等。不少問題都能通過這些方法得到非平凡的查詢復雜性下界。
量子交互計算復雜性。量子交互計算復雜性理論包括量子交互式證明系統和量子通信復雜性。這一方面是經典計算復雜性在量子計算時代的進一步發展,另一方面也是滿足當今量子信息與量子計算科學發展的需求。從現有技術來看,量子計算機的研制和維護成本高昂,未來量子計算或將以云計算的形式給一般用戶提供服務。通過連接多個中等規模量子計算機,搭建量子網絡實現高效的量子計算;將經典計算機或者小規模量子計算機連接到網絡并與之交互,獲得更強的量子計算能力是目前量子信息科學研究的一個主流方案。荷蘭科學家Wehner等人在《科學》期刊撰文[6] 為這個量子計算方案給出一個清晰的發展綱領。量子交互計算復雜性為量子網絡方案提供了理論框架。
量子機器學習。廣義的來說,量子機器學習的研究包括兩個方面:(1)利用量子計算技術提升經典機器學習方法,(2)利用經典機器學習方法解決量子力學領域的問題。目前這兩方面的研究都受到了很大關注。狹隘的量子機器學習僅指上面第一點,這也是本報告所關注的。目前,研究者對機器學習領域的一些主要模型和方法都進行了量子化,即參考經典機器學習算法建立對應的量子算法。這些量子機器學習算法有些可以進行嚴格的理論分析,有些則是啟發式的,依賴于實驗分析。量子機器學習領域早期的發展很大程度是源于解線性方程組量子算法(HHL算法)的提出,而近期的研究工作更多集中在基于變分量子電路的算法方面。量子計算與AI的交叉研究值得進行深入探索,不過目前一些量子機器學習方面的研究有待更嚴肅的理論分析。
量子優化算法。與其他量子算法類似,量子優化的關注點仍然是量子計算的優勢,即如何利用量子技術來對經典優化方法進行加速。目前量子優化領域相對于經典方法的加速效果主要體現在函數估值的查詢復雜度上。另一方面,近年陸續有小規模或專用的量子計算機問世,無法嚴格理論分析優勢的量子啟發式優化算法得到了實驗驗證的可能,因此也有針對這方面的研究。
量子電路優化與經典模擬。目前由于量子計算機尚在實驗研發階段,量子比特個數、可實現的量子電路深度和規模都非常有限,所以現階段的研究更應該關注在小規模量子電路的設計與優化上。本文將涉及淺層量子電路的優勢、特定量子門構成的量子電路復雜性、受物理硬件結構限制的量子電路優化方法、量子隨機電路的經典模擬算法等四個方面的研究進展。
需要指出的是,以上五方面的內容并非完全獨立,本文只是相對集中的把它們分成五部分以便組織撰寫。首先,量子通信復雜性與量子查詢復雜性緊密相關。相比量子查詢復雜性,在量子通信復雜性模型中,我們對參與方的局部計算能力不作任何限制,因此這個模型的表達能力更強,計算更加復雜。其次,量子機器學習和量子優化方向的很多算法都是從查詢復雜性方面體現量子優勢,因此本質上他們是量子查詢算法。同時,從經典計算領域來看,優化是機器學習的技術基礎,因此量子優化技術自然可以用來提升機器學習問題的求解。
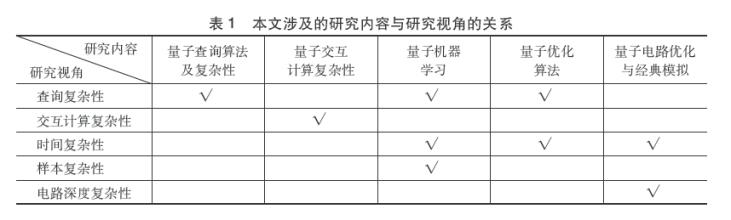
另外,以上幾個方面的研究內容也并不完全與前面五個研究視角一一對應。下面用表1把以上五方面的研究內容和五個研究視角的關系更清晰的表示出來,其中打勾表示有關系。例如,量子機器學習既可以從時間復雜性方面進行分析,也可以從查詢復雜性角度考慮,還可以討論樣本復雜性問題。再如量子電路優化,如果我們關注的是基本門的個數,那本質上體現的是對應算法的時間復雜性,如果關注的是邏輯門的層數則體現的是電路深度復雜性。
當前,量子技術已經進入到NISQ時代 (帶噪音中等規模量子技術,Noisy Intermediate-Scale Quantum Technology)[7]。如何基于現有的量子技術把量子計算推上實用不僅僅是技術問題,也面臨計算理論上的挑戰。它給理論計算機學家們提出了這樣一個科學問題“如何利用帶噪音的中等規模量子計算機實現高效和可靠的量子計算”。同時,量子計算領域的遠期目標是實現通用量子計算,要達此目標量子糾錯是至關重要且充滿挑戰的一步。目前在量子糾錯的理論方面已經取得了豐富成果。由于量子糾錯的重要性和內容的豐富性,需要一篇專門的文章才足以承載,因此本文不對此進行介紹,但我們應認識到其重要性所在。
[1] A Ambainis and R Freivalds. 1-way quantum finite automata: strengths, weaknesses and generalizations [C]. In: Proceedings of the 39th Annual Symposium on Foundations of Computer Science, Palo Alto, 1998. 332–341.
[2] A Ambainis and N Nahimovs. Improved constructions of quantum automata. Theor Comput Sci, 2009, 410: 1916–1922.
[3] D Qiu, L Li, P Mateus and A Sernadas. Exponentially more concise quantum recognition of non-RMM regular languages[J], Journal of Computer and System Sciences. 2015, 81: 359–375.
[4] 李綠周,量子計算研究要“軟硬兼施”,《中國科學報》 (2020-05-07 第3版 信息技術),http://www.sdshimeng.com/teamwork/showPostMessage.html?id=7871
[5] 孫曉明, 量子計算若干前沿問題綜述. 中國科學: 信息科學, 2016, 46: 982.
[6] S Wehner, D Elkouss, and R Hanson. Quantum internet: A vision for the road ahead [J]. Science, 2018. 362(6412):eaam9288.
[7] J Preskill. Quantum Computing in the NISQ era and beyond [J]. Quantum, 2018. 2:79.


