本次分享由安春燕團隊投稿在 DASFAA 2024的論文《AoSE-GCN: Attention-aware Aggregation Operator for Spatial-Enhanced GCN》。該論文一作是2022級研究生葉家震,通訊作者是安春燕。該論文提出了一個名為Latt的注意力感知聚合算子(attention-aware aggregation operator)并從空間角度提出了鄰域聚合增強的AoSE-GCN模型。AoSE-GCN彌補了GCN在捕捉局部鄰域細節(jié)的不足,同時包含了拉氏算子天然攜帶的全局結(jié)構(gòu)視野,使其可以感知圖網(wǎng)絡(luò)全局和局部兩種不同的域。此外,該文章為我們研究GCN等譜圖網(wǎng)絡(luò)提供了一種從空間增強的新視角。
摘要:圖神經(jīng)網(wǎng)絡(luò)(Graph Neural Networks, gnn)在各種與圖相關(guān)的應(yīng)用中取得了顯著的成功,大致可分為基于空間和基于頻譜的方法。特別是,空間方法可以很好地捕獲局部鄰域,但缺乏全局結(jié)構(gòu)洞察力,因為它們是基于聚合算子在局部節(jié)點上定義的。相反,光譜方法包含全局結(jié)構(gòu)信息,但由于拉普拉斯矩陣的性質(zhì)而難以獲得局部細節(jié)。值得注意的是,頻譜方法在濾波器上采用頻率分量調(diào)整來實現(xiàn)有效的卷積,但與空間方法相比,它們?nèi)匀徊荒敲挫`活。挑戰(zhàn)在于平衡這些方法,使GNN模型能夠捕獲全局級和局部級信息,從而促進圖表示學習。為了解決這個問題,我們引入了一個新的注意力感知聚合算子,表示為Latt,通過在拉普拉斯矩陣中附加注意力得分作為附加權(quán)重。受其優(yōu)點的啟發(fā),我們將Latt集成到GCN模型中,以感知不同層次的場,稱為AoSE-GCN。值得注意的是,我們的Latt并不局限于GCN,任何光譜方法都可以很容易地插入。在基準數(shù)據(jù)集上的大量實驗驗證了AoSE-GCN在全監(jiān)督或半監(jiān)督設(shè)置下節(jié)點分類任務(wù)的優(yōu)越性。
圖神經(jīng)網(wǎng)絡(luò)(GNN)在各種與圖相關(guān)的應(yīng)用中取得了顯著的成功,包括社會分析[3]、流量預(yù)測[12]和推薦系統(tǒng)[4]。它們有效學習圖中復雜關(guān)系的能力使其適用于節(jié)點分類 [32,19]、鏈接預(yù)測[26]和圖分類[1]等任務(wù)。
各種類型的GNN已經(jīng)被開發(fā)出來[13,30,2,7,19,24],根據(jù)卷積算子可以將其分為空間域和譜域圖卷積。在空間域中,直接在節(jié)點域中定義卷積,使用聚集算子收集局部鄰域信息來學習節(jié)點表示。這個過程通常通過消息傳 遞框架[11]進行封裝和泛化。例如,GraphSAGE[13]通過隨機抽樣聚合加 權(quán)的相鄰節(jié)點,生成節(jié)點表示。類似地,GAT[30]基于注意機制計算相鄰 節(jié)點的權(quán)重,MoNet[24]通過平均相鄰節(jié)點上定義的加權(quán)函數(shù)來學習節(jié)點 表示。雖然這些方法對于捕獲局部節(jié)點鄰域的信息是有效的,但它們往往 忽略了對全局結(jié)構(gòu)的洞察。另一方面,光譜方法包含全局結(jié)構(gòu)信息,但由 于拉普拉斯矩陣的性質(zhì),往往難以獲得局部細節(jié)。頻譜GNN基于卷積定理定義卷積。例如,SCNN[2]全局使用拉普拉斯特征分解在譜域進行圖表示, 而不是局部化。此外,ChebyNet[7]和GCN[19]使用Chebyshev多項式作為 卷積核參數(shù),實現(xiàn)了局部卷積。為了更有效地捕獲局部結(jié)構(gòu)的信息, ChebyNet- II[15]通過Chebyshev插值增強了原始ChebyNet的逼近能力。 BernNet[14]模型采用Bernstein多項式來近似圖濾波器的頻率響應(yīng),使其能夠?qū)W習任意濾波器。GPR-GNN[6]模型通過基于單項的圖卷積近似來推導 低通或高通濾波器。雖然頻譜方法調(diào)整濾波器的頻率成分以獲得有效的卷積,但與空間域方法不同,它們在直接和靈活地從空間背景下的局部鄰域 結(jié)構(gòu)中聚合信息方面面臨挑戰(zhàn)。因此,在這些方法之間取得平衡對于釋放基于圖的學習的全部潛力至關(guān)重要。
為了研究全局結(jié)構(gòu)信息的最佳利用和局部相鄰細節(jié)的靈活聚集,我們通過光譜方法的空間解釋來解決這個問題。頻譜方法通過調(diào)整濾波器頻率 分量有效地實現(xiàn)卷積,其中局部聚集中相鄰節(jié)點的權(quán)重與這些頻率分量權(quán) 重的調(diào)整很好地對應(yīng),正如Chen[5]在一項全面調(diào)查中所強調(diào)的那樣。此外,MPNN[11]提供了頻譜方法的簡潔總結(jié),使用拉普拉斯矩陣多項式來捕獲 消息傳遞過程中的局部結(jié)構(gòu)。在這個過程中,拉普拉斯矩陣作為圖拉普拉 斯算子[28],在卷積逼近中包含全局和局部信息。值得注意的是,在 ChebyNet和GCN等近似卷積過程中,可以繞過拉普拉斯矩陣的特征值分解, 從光譜方法的空間角度來看,使其更類似于聚合算子。然而,必須注意的是,該算子僅限于捕獲基本的鄰域節(jié)點關(guān)系,從而限制了其有效性。
為了解決這些挑戰(zhàn),我們提出了一種新穎的注意力感知聚合算子,表示為 Latt,其中注意力得分作為額外的權(quán)重附加。這種添加允許在拉普拉斯矩陣的 鄰域節(jié)點之間調(diào)整擾動增益。為了實證證明聚合算子Latt的有效性,我們將其 無縫集成到圖卷積網(wǎng)絡(luò)(GCN)模型中,從而增強了空間域內(nèi)的近似卷積過程。 特別地,我們引入了一種新的GCN變體,稱為AoSE-GCN,它使用Latt代替拉 普拉斯矩陣來捕獲局部鄰域內(nèi)的有效信息。這種戰(zhàn)略替代確保了我們的模型 不僅封裝了全局信息,而且還識別了局部結(jié)構(gòu)內(nèi)鄰近節(jié)點的重要性。值得注意的是,我們設(shè)計的聚合算子并不僅僅局限于GCN模型,它通過對拉普拉斯 矩陣的微小修改,提供了與各種光譜方法集成的多功能性。
我們的貢獻可以總結(jié)如下:
在空間圖神經(jīng)網(wǎng)絡(luò)(GNNs)中,卷積是在節(jié)點域中定義的,展示了利用各種聚合函數(shù)靈活捕獲局部鄰域信息的非凡能力。例如,GraphSAGE[13]采用鄰域節(jié)點 的隨機抽樣和一組不同的聚類函數(shù)來進行節(jié)點表示學習。GAT[30]利用注意機制定義聚合函數(shù),實現(xiàn)有效的節(jié)點表示學習。DCNN[1]利用從隨機行走中獲 得的K-hop轉(zhuǎn)移概率作為節(jié)點間的權(quán)重聚合。GAM[22]采用注意機制引導的隨機行走對有效節(jié)點進行采樣,捕獲圖結(jié)構(gòu)中的關(guān)鍵區(qū)域連通性信息。 ConfGCN[29]為每個節(jié)點學習一個置信度函數(shù),影響節(jié)點相關(guān)性并修正聚合函數(shù)。HGNN[9]將邊緣擴展為連接多個節(jié)點的超邊緣,并定義超邊緣上的聚合函數(shù),用于節(jié)點特征傳播。MoNet[24]將每個節(jié)點的局部結(jié)構(gòu)映射到相同大小的向量,并在映射結(jié)果上學習共享卷積核。PGC[34]定義了一個采樣函數(shù)來構(gòu)建節(jié)點鄰域,并與卷積過程的特定加權(quán)函數(shù)相乘。
雖然空間方法在捕獲鄰域信息方面表現(xiàn)出豐富而靈活的手段,但它們的重點往往放在局部鄰域上,往往忽略了全局結(jié)構(gòu)的洞察力。相比之下, 我們提出的方法引入了注意力感知聚合算子Latt來近似卷積操作。這一創(chuàng)新允許同時考慮全局視圖和局部結(jié)構(gòu),有效地補償了空間方法在全局洞察力 方面的局限性。
譜圖神經(jīng)網(wǎng)絡(luò)(GNNs )基于譜圖理論定義圖卷積,通過學習濾波器調(diào)整頻率分量,實現(xiàn)有效的卷積。SCNN[2]開創(chuàng)了譜域圖卷積,直接學習圖卷積的濾 波器系數(shù)。GCN[19]使用一階切比雪夫多項式近似,被認為是一種有效的 低頻濾波器。GraphHeat[32]增強低頻濾波器,并使用熱核抑制高頻波。 APPNP[20]和GDC[21]使用perpersonalized PageRank (PPR)設(shè)置低頻濾波的過濾權(quán)值。GNN-LF/HF[37]設(shè)計濾波器,從圖形優(yōu)化器的角度模擬高通和低通濾波器。ChebNet[7]采用切比雪夫多項式近似濾波運算來學習任意濾 波器。Chebynet-II[15]通過切比雪夫插值增強了切比雪夫多項式近似,以更好地學習任意圖卷積。GPR-GNN[6]通過圖卷積的基于單項式的近似派 生出低通或高通濾波器。BernNet[14]使用Bernstein多項式來近似圖濾波器 的頻率響應(yīng),使其能夠?qū)W習任意濾波器。
雖然這些頻譜方法專注于學習有效濾波器,但它們通常不如空間方法靈活,后者直接從空間角度定義卷積ag-gregates。在我們的方法中,我們引入了注意力感知聚合算子Latt作為拉普拉斯算子在逼近卷積運算中的替代 品。Latt直接在空間域上使用注意算子有效地執(zhí)行局部聚合,與傳統(tǒng)的光譜方法相比,提供了更強的靈活性。
有很多方法專門用于不同類型的圖,包括同構(gòu)圖和異構(gòu)圖。例如,GCN和 Graph-SAGE專注于同構(gòu)圖。此外,還提出了許多方法,如HetGNN[36]、 RGCN[26]、HAN[31]等,來學習異構(gòu)圖表示。例如,Metapath2vec[8]通過 基于元路徑和隨機漫步策略捕獲不同類型節(jié)點和關(guān)系的結(jié)構(gòu)和語義相關(guān)性來學習圖表示。HIN2vec[10]在異構(gòu)網(wǎng)絡(luò)中探索豐富的信息和網(wǎng)絡(luò)結(jié)構(gòu)。
通過捕獲節(jié)點之間的多個元路徑。HetGNN[36]通過帶重啟策略的隨機行走 對節(jié)點的異構(gòu)鄰居進行強相關(guān)采樣,并聚合這些鄰居信息,生成最終的節(jié)點 em- bedingrepresentation。R-GCN[26]分別學習不同類型關(guān)系下節(jié)點的節(jié)點表 示,最后疊加更新最終節(jié)點嵌入表示。HAN[31]通過學習節(jié)點級和語義級的關(guān)注,充分考慮了節(jié)點和元路徑的重要性,增強了模型學習異構(gòu)圖節(jié)點表示 的能力。值得注意的是,很少有文獻探討空間/光譜GNN 與異構(gòu)圖的結(jié)合。在應(yīng)用拉普拉斯算子進行鄰居信息聚合時,如何設(shè)計融合異構(gòu)節(jié)點和邊緣信息的GNN模型是一個挑戰(zhàn)。
無向圖通常定義為G = (V, E), V表示一組節(jié)點,E表示一組邊。設(shè)A表示鄰 接矩陣,Aij表示圖G的節(jié)點i和節(jié)點j之間的連接,D表示度矩陣,Dii = 求和 A i j。 因此,圖拉普拉斯矩陣 可以定義為L = D−A,它的標準和規(guī)范化形式通常表示為L ~ =In−D−1/2 AD− 1/2,其中In是一個單位矩陣。由于L ~是一個實對稱的正半定矩陣,它可以被 特征分解為L ~ = UΛU−1,其中U是由特征向量組成的酉矩陣,Λ是由特征值組成的對角矩陣。根據(jù)圖信號理論,信號x∈R n在圖G上的卷積運算定義 為y =UgθUTx,其中g(shù)θ 為卷積核,y表示信號x經(jīng)過卷積運算后的結(jié)果。
基于圖信號理論的圖卷積方法需要對拉普拉斯矩陣進行特征分解,耗時長, 且不能保證局部連接。幸運的是,Chebynet和GCN通過使用拉普拉斯算子的 多項式近似卷積操作來避免這些弱點。接下來,我們將介紹兩種基本的譜方 法。
Chebynet。ChebyNet直接將卷積核替換為k階Chebyshev多項式[7],其定義如下:

式中Tk為第k項Chebyshev多項式,θk為第k項多項式的系數(shù)。它將圖卷積運 算簡化為拉普拉斯矩陣L的Chebyshev多項式的和,避免了L的特征分解,同時通過多項式性質(zhì)保持卷積的局域化。最后,Chebynet的卷積定義如下:
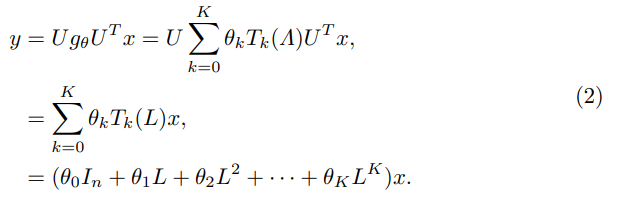
一般GCN。GCN通過簡化Chebynet,使用一階Chebyshev多項式近似進行圖 卷積,即設(shè)k = 1, θ= θ0=−θ1,卷積定義如下:
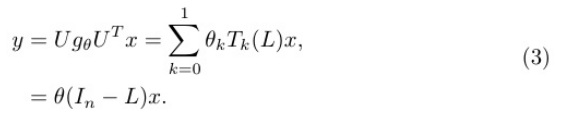
離散拉普拉斯算子從周圍節(jié)點的梯度差中得到中心節(jié)點的擾動增益效應(yīng)。同樣,拉普拉斯矩陣L是圖G上拉普拉斯算子的離散對應(yīng),它描述了圖[28]上節(jié)點的擾動增益效應(yīng)。重要的是要注意,分析拉普拉斯矩陣的擾動增益揭示了 圖的局部和全局屬性,以及節(jié)點之間的關(guān)聯(lián)程度。
在局部性質(zhì)中,我們得到節(jié)點j∈Ni對節(jié)點i的擾動增益△f i,其中△為 拉普拉斯運算符號,f∈R n表示圖G上的任意節(jié)點信號,Ni為圖中節(jié)點i的一 個鄰域。計算如下:
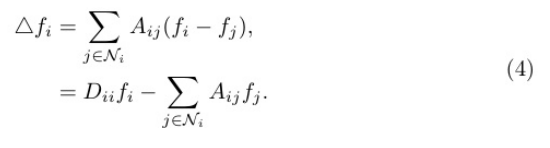
在全局屬性中,我們可以得到整個圖G中每個節(jié)點的擾動增益值。我們用F = (f1,f2,···fn ))來表示圖G具有全部N個節(jié)點的信號,圖的擾動增益表示為
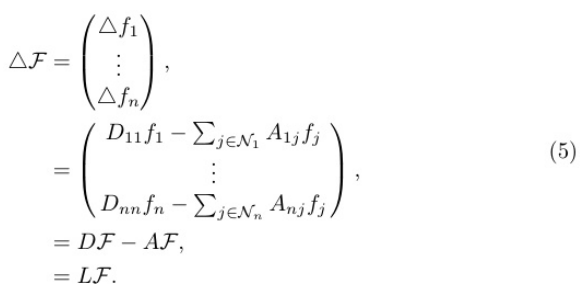
從兩個性質(zhì)點可以看出,拉普拉斯矩陣揭示了圖結(jié)構(gòu)上局部節(jié)點之間 的關(guān)聯(lián)和全局節(jié)點之間的關(guān)聯(lián)。在拉普拉斯矩陣的計算中,圖中的每個節(jié)點i與其相鄰節(jié)點的特征進行直接聚合。因此,拉普拉斯矩陣可以概念化為作用于空間域內(nèi)圖的一個聚集算子,它只是一個簡單的直接聚集。
考慮到拉普拉斯矩陣特征值分解的耗時問題,有必要將原始卷積核簡化為 多項式核。特別是,我們利用卷積近似以拉普拉斯矩陣多項式乘積與圖信 號相乘的形式代替卷積核(參見Eq. 2和3)。另一方面,拉普拉斯矩陣可以很 好地表示節(jié)點之間的關(guān)系,以捕獲全局結(jié)構(gòu)信息。在對目標節(jié)點的鄰居特 征進行聚合時,受拉普拉斯矩陣空間聚合的影響,可將其視為一個空間聚 合算子(參見Eq. 4和5),但其有效區(qū)分不同鄰居的能力有限。因為它主要捕 獲簡單的鄰居關(guān)系。為了解決這一限制,我們創(chuàng)新地設(shè)計了一個注意力感 知聚合算子,從空間角度取代了原來的拉普拉斯矩陣。該算子在增強頻譜 GNN模型的能力方面起著關(guān)鍵作用。
隨后的部分將詳細介紹注意力感知聚合算子,闡明其功能,并強調(diào)如 何將其無縫集成到頻譜GNN模型中以增強性能。
基于Eq. 4的見解,通過拉普拉斯計算獲得的節(jié)點擾動的增益被表述為加權(quán)集合,對其相鄰節(jié)點的加權(quán)求和。為了方便這個過程,我們引入了一組可學習 的參數(shù),表示為µij。這些參數(shù)作為注意力放大系數(shù),在聚合過程中動態(tài) 捕捉相鄰節(jié)點j對中心節(jié)點i的影響。
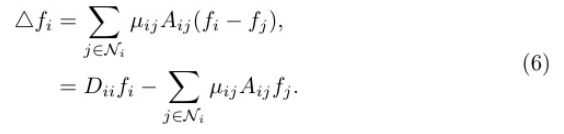
因此,對于圖中所有N個節(jié)點,整個圖的攝動增益表示為△F。
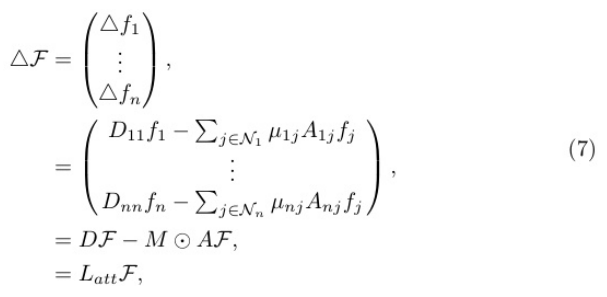
其中Latt= D−M⊙A表示替換拉普拉斯矩陣的注意力感知聚合算子。M是 一個關(guān)注矩陣Mij=µij,其結(jié)構(gòu)與鄰接矩陣a相同,值得注意的是,Mij=Mji 表示M是不對稱的。與Eq. 5中的拉普拉斯矩陣相反,Latt的參與導致了這 種不對稱性,從而破壞了拉普拉斯矩陣的頻譜分解。因此,我們將Latt單獨作為一個空間增強的聚合算子進行強制。特別是,受圖注意力網(wǎng)絡(luò) (GAT)模型[30]的啟發(fā),我們采用了一種注意力機制來動態(tài)計算每個相鄰 節(jié)點的注意力系數(shù)µij,如下所示:
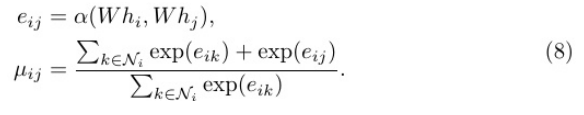
其中hi∈RF表示節(jié)點i的特征,F(xiàn)表示節(jié)點特征的通道數(shù),W∈RF’×F是可學習的線性變換參數(shù),α(·)是單層前饋神經(jīng)網(wǎng)絡(luò)。eij計算節(jié)點I和節(jié)點j之間的關(guān)聯(lián)程度∈Ni。µij是我們上面提到的注意力放大系數(shù),取值范圍在[1, 2]中。
Latt引入的基本創(chuàng)新在于,在拉普拉斯矩陣框架內(nèi),在計算圖中每個 節(jié)點的擾動增益時,將注意力得分作為補充權(quán)重。這個算子的設(shè)計是為 了解決拉普拉斯矩陣的局限性,傳統(tǒng)上,它捕捉的是直接的本地關(guān)系。通過無縫集成注意力分數(shù),Latt增強了 節(jié)點聚合的適應(yīng)性,在本地聚合過程中提供了一種更靈活的機制來捕獲和整 合來自相鄰節(jié)點的細微信息。
將聚合算子Latt引入到譜GCN模型中,得到AoSE-GCN模型,該模型通過空間聚合進行圖表示學習,增強了GCN模型。特別地,我們使用隨機游走歸一化將Latt表示為Lrwatt = In−D−1 (M⊙A),并將其代入Eq. 3,作為原始拉普拉斯矩陣的替換:
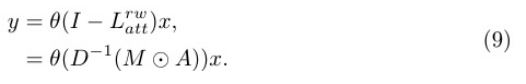
隨后,我們采用重整化技巧[19],將D−1 (M⊙a)替換為a ~ att。最后,我們有:
![]()
當將圖信號擴展到每個節(jié)點特征向量具有f維的節(jié)點特征矩陣X∈Rn×F時, 卷積操作定義如下:
![]()
其中H (r)∈Rn×F′為第r層的卷積輸出特征,H (0) = X, W (r)∈RF′×C ′ 為第r層的可學習權(quán)參數(shù)矩陣。形式上,我們認為雙層AoSE-GCN為:
![]()
Y∈R n×C表示節(jié)點分類的預(yù)測結(jié)果。
AoSE-GCN的關(guān)鍵創(chuàng)新在于用注意力感知聚合算子取代傳統(tǒng)的拉普拉斯 近似卷積算子。該算子賦予全局視角,并為每個鄰域節(jié)點分配不同的注意力 分數(shù)。通過這樣做,AoSE-GCN在局部聚合過程中獲得了識別和考慮單個鄰 域節(jié)點重要性的能力。這種向個性化注意力分數(shù)的轉(zhuǎn)變促進了圖數(shù)據(jù)中信息 聚合和傳播的更適應(yīng)性、更精確和更靈活的過程。值得注意的是,我們的Latt 并不局限于GCN,任何光譜方法都可以很容易地插入。
我們使用交叉熵損失函數(shù)來量化節(jié)點分類任務(wù)中預(yù)測結(jié)果和實際結(jié)果之間的差異。
![]()
其中C是類的數(shù)量,yL是帶標簽的節(jié)點索引集。Ylc表示屬于c類的節(jié)點l的實際 標簽值,Yˆlc為對應(yīng)的預(yù)測概率值。
在本節(jié)中,我們評估了AoSE-GCN的性能,并將其與幾個公共圖數(shù)據(jù)集上的基 線模型進行了比較。此外,為了突出注意力感知聚合算子Latt的有效性,我們將它們與頻譜GNN(即Chebynet和GCN)集成,以評估它們的性能。最后,我們可視化了不同模型的學習嵌入,以說明我們方法的優(yōu)勢。
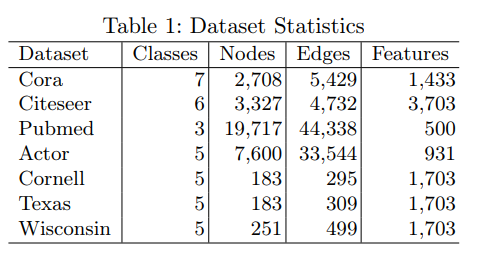
為了評估我們方法的有效性,我們在不同的數(shù)據(jù)集上進行了半監(jiān)督和完全監(jiān)督 的實驗。表1提供了數(shù)據(jù)集統(tǒng)計的概述。我們還提供了每個數(shù)據(jù)集的詳細解釋, 并描述了我們實驗中使用的具體數(shù)據(jù)分區(qū)。
半監(jiān)督數(shù)據(jù)集。我們利用Cora、Citeseer和Pubmed[27]這三個廣泛使用的引文網(wǎng)絡(luò)數(shù)據(jù)集進行半監(jiān)督節(jié)點分類。在引文網(wǎng)絡(luò)中,圖結(jié)構(gòu)保持同構(gòu),其中節(jié)點表示文檔,邊表示文檔之間的引文關(guān)系。每個節(jié)點都與特征嵌入相關(guān)聯(lián),特征嵌入對相應(yīng)文檔中的代表性單詞進行編碼。為了進行我們的半監(jiān)督實驗,我們遵循了將數(shù)據(jù)集[35]分成訓練集、驗證集和測試集的既定方法。具體來說,對于 數(shù)據(jù)集中的每個類,我們使用每個類20個節(jié)點進行訓練,500個節(jié)點進行驗證, 1000個節(jié)點進行測試。

全監(jiān)督數(shù)據(jù)集。我們使用了一個名為actor[16]的行動者共現(xiàn)網(wǎng)絡(luò)以及三個網(wǎng) 頁數(shù)據(jù)集:Cornell, Texas和wisconsin -sin[25],用于完全監(jiān)督節(jié)點分類。Actor 數(shù)據(jù)集捕獲從維基百科頁面中提取的參與者之間的共現(xiàn)關(guān)系,其中節(jié)點特征 是基于從參與者各自的維基百科頁面中獲得的相關(guān)關(guān)鍵字構(gòu)建的。在網(wǎng)頁數(shù) 據(jù)集中,節(jié)點表示不同網(wǎng)頁之間的超鏈接,每個節(jié)點的特征對應(yīng)于與網(wǎng)頁內(nèi) 容相關(guān)的代詞的嵌入表示。為了確保標準化的方法,我們遵循了先前研究中 提出的方法來進行完全監(jiān)督的實驗。具體來說,對于每個數(shù)據(jù)集,我們將每 個類的節(jié)點隨機劃分為訓練集(60%)、驗證集(20%)和測試集(20%)。所有模 型的性能在10個隨機分割的測試集上進行測量。
為了評估我們方法的有效性,我們與幾種成熟的深度學習方法進行了比較實 驗。LP (Label Prop-agation)[38]采用高斯隨機場模型來探索結(jié)構(gòu)和標簽信息。 JK-Net[33]通過考慮每個節(jié)點不同的鄰域范圍,利用密集連接來改進學習表 示。Chebynet[7]使用Chebyshev多項式近似有效地執(zhí)行譜圖卷積。GCN[19]是 Chebynet的簡化,只關(guān)注一階Chebyshev多項式。GAT[30]采用注意機制學習不同的節(jié)點權(quán)重得分。
對于包括LP、JK-Net和GAT在內(nèi)的幾種基線方法,我們使用文章[17]中報告 的結(jié)果進行比較。對于其余的方法,我們根據(jù)作者指定的pa- parameter設(shè)置 在我們的實驗環(huán)境中手動實現(xiàn)。此外,為了進一步有效地演示所提出的注意 力感知聚合算子Latt,我們簡單地將其合并到Chebynet模型中,命名為AoSEChebynet,以進行比較。
對于半監(jiān)督和全監(jiān)督實驗的評價任務(wù),我們設(shè)置Adam SGD[18]作為優(yōu) 化算法。在訓練過程中,我們通過監(jiān)測驗證集上的最佳訓練性能,以固定 的epoch數(shù)實現(xiàn)早期停止,以減輕過度擬合的風險。我們使用模型隱藏層的 L2范數(shù)和權(quán)重衰減系數(shù)作為損失函數(shù)的懲罰項,這提高了模型的泛化能力。 對于我們模型中使用的超參數(shù),表2總結(jié)了AoSE-GCN,它在驗證數(shù)據(jù)集上達到了最佳性能。
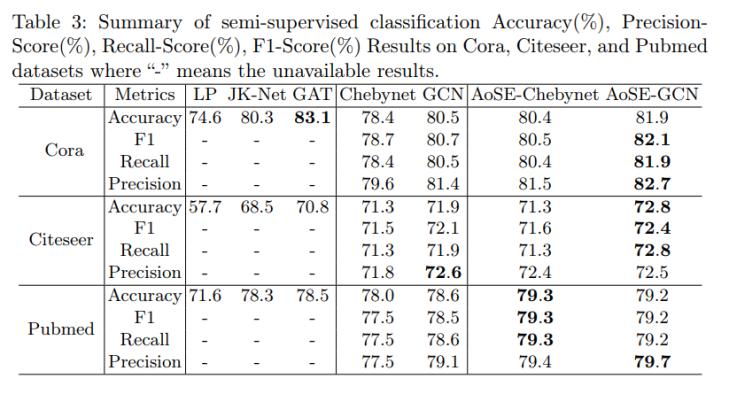
表3給出了半監(jiān)督分類的各種指標的結(jié)果。正如我們所看到的,就所有指標 而言,AoSE-GCN比基線GCN模型表現(xiàn)得更好。同樣,與Chebynet基線模型 相比,AoSE-Chebynet也獲得了具有競爭力的結(jié)果。這一觀察得出的結(jié)論是, 我們的注意力感知聚合算子有效地增強了像GCN和Chebynet這樣的模型, 它們都依賴于Chebyshev多項式近似的卷積。當應(yīng)用于同構(gòu)圖數(shù)據(jù)集時,這種增強尤為顯著。
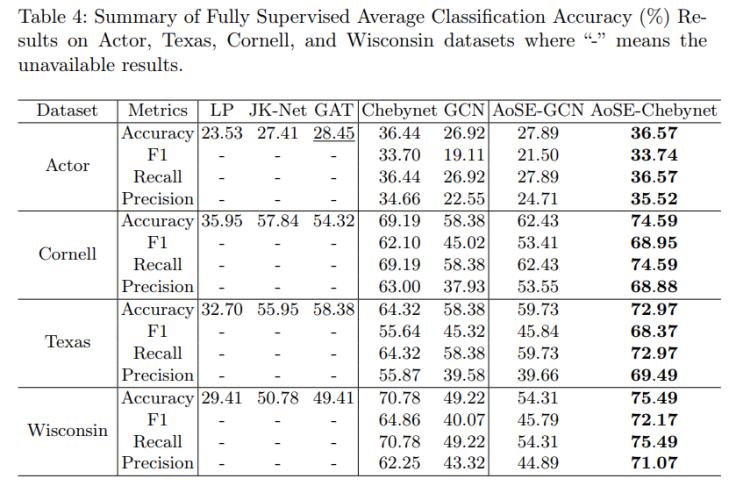
在表4中,我們給出了異構(gòu)圖數(shù)據(jù)集上完全監(jiān)督節(jié)點分類的結(jié)果。值得注意的是,基線模型Chebynet在異構(gòu)圖結(jié)構(gòu)上下文中驚人地優(yōu)于GCN方法。 這種現(xiàn)象可能歸因于GCN模型是拉普拉斯平滑的一種特殊情況,它可以更 快地進行過度平滑,特別是在較小的數(shù)據(jù)集上,如[23]所示。然而,AoSEGCN和AoSE-Chebynet模型的引入證明了這一點,應(yīng)用于異構(gòu)圖時,與基本模型相比,性能上的改進。
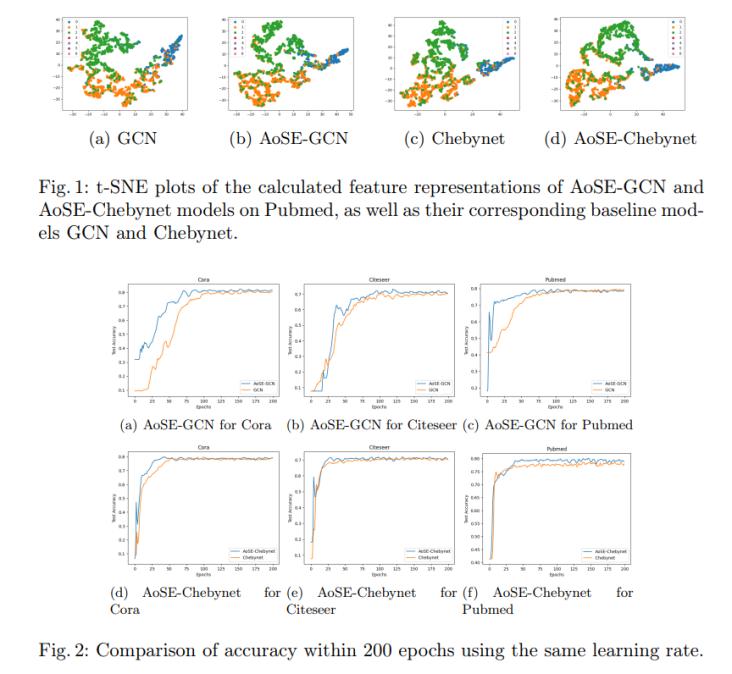
在圖1中,我們使用t-SNE來可視化地表示我們的模型和基本模型在Pubmed 數(shù)據(jù)集上提取的節(jié)點嵌入。我們可以通過Latt改進的模型,即AoSE-GCN和 AoSE-Chebynet,可以更好地分離不同的節(jié)點組。這意味著Latt通過同時考慮 全局和局部信息來提示圖表示學習。
此外,我們在圖2中比較了基本模型和增強模型在學術(shù)數(shù)據(jù)集上的收斂速度。我們觀察到AoSE-GCN和AoSE-Chebynet具有更快的收斂速度。這可以歸因于鄰域特征的加權(quán)聚合。
通過深入研究拉普拉斯矩陣在GNN聚合過程中的關(guān)鍵作用,我們的創(chuàng)新采用 了注意力感知聚合算子的形式,旨在取代拉普拉斯矩陣的傳統(tǒng)使用。該算子 無縫集成到圖卷積網(wǎng)絡(luò)(GCN)模型中,從而產(chǎn)生了新的AoSE-GCN方法。Latt 的結(jié)合。
授權(quán)模型通過注意機制選擇性地聚合相鄰信息。從空間角度來看,這一添 加有效地提升了GCN和Chebynet等經(jīng)典GNN模式。在未來的工作中,我們 的目標是通過將AoSE-GCN與剩余機制和多尺度機制等先進技術(shù)協(xié)同作用 來解決平滑問題。